Research

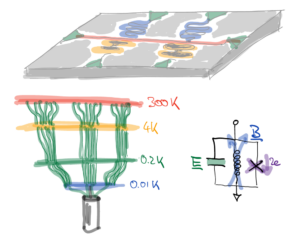
Quantum Device & System Engineering

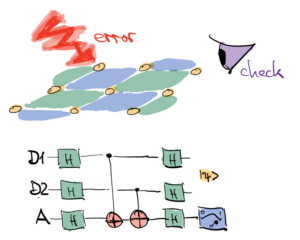
Quantum Error Correction & Algorithms

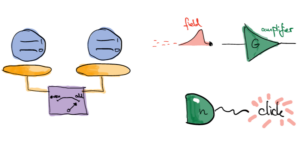
Quantum Measurements & Amplification

Elements of Quantum Networks

Device Architecture & Fabrication

Quantum Science & Machine Learning

Hybrid Quantum Systems

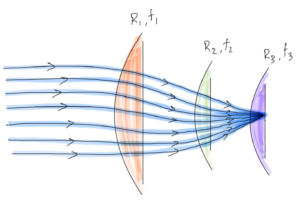
Optical Simulation & Design